Probabilidade: Terceira Parte
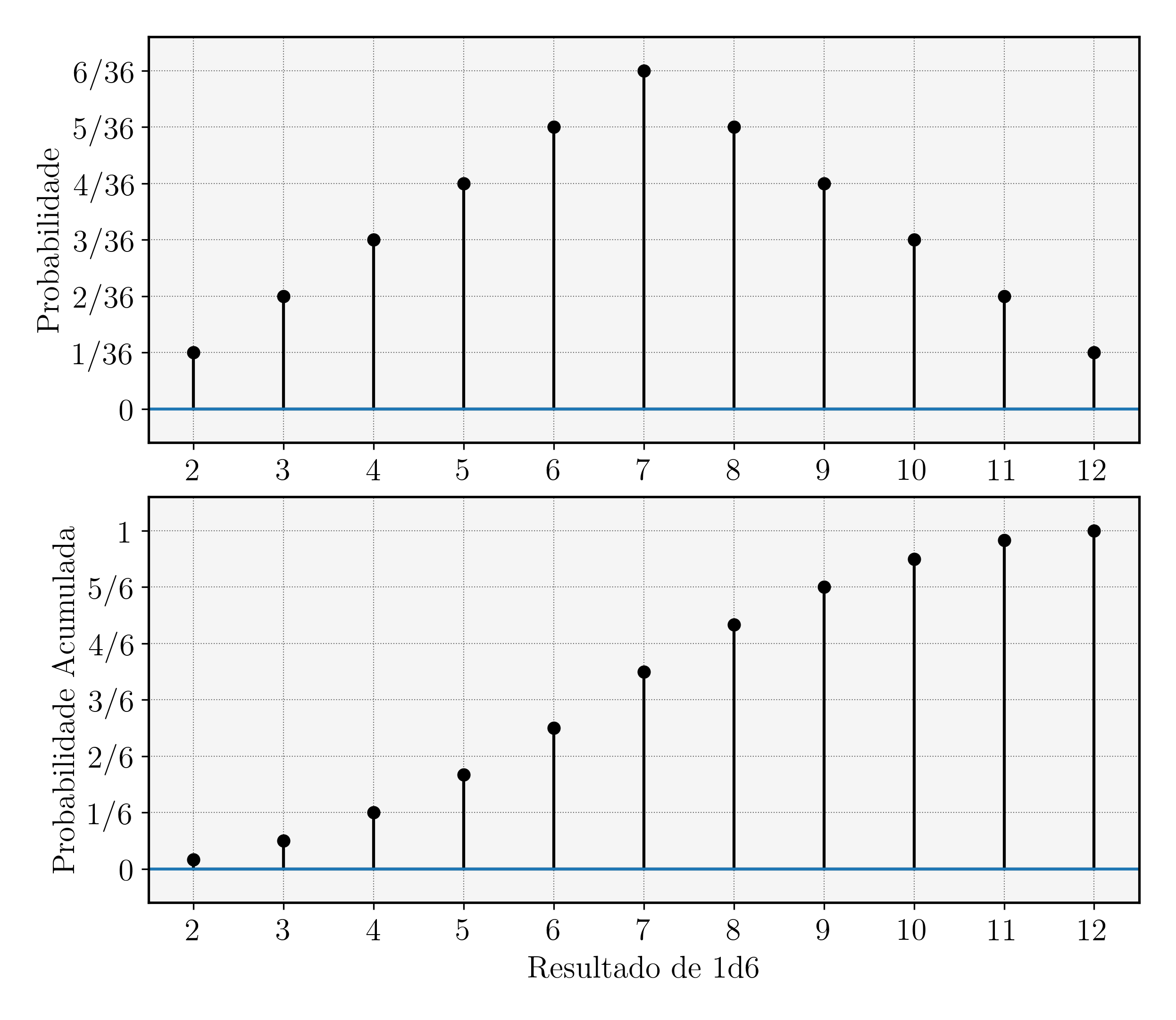
Muitos designers consideram que uma distribuição uniforme – como vista no último artigo – é imprevisível demais. Há alguma razão nisso (nós ainda vamos ver por quê), e, para eles, é necessário combinar alguns dados, para tornar a distribuição de probabilidades mais adequada e, talvez, mais realista. Por exemplo, alguns sistemas somam o resultado de dois dados de 6 faces ou, em notação rpgística: 2d6. A tabela abaixo mostra o resultado desse procedimento, e o gráfico vai logo em seguida. Note que eu dei uma aumentada na altura do gráfico – se eu não fizesse isso, seria muito difícil ver as probabilidades.
| Resultado | Probabilidade | Probabilidade Acumulada |
|---|---|---|
| 2 | 1/36 | 2/36 |
| 3 | 2/36 | 3/36 |
| 4 | 3/36 | 6/36 |
| 5 | 4/36 | 10/36 |
| 6 | 5/36 | 15/36 |
| 7 | 6/36 | 21/36 |
| 8 | 5/36 | 26/36 |
| 9 | 4/36 | 30/36 |
| 10 | 3/36 | 33/36 |
| 11 | 2/36 | 35/36 |
| 12 | 1/36 | 36/36 |
Como esse exemplo pode ajudar na construção do seu sistema?
Para analisar, vamos imaginar um sistema em que um teste bem-sucedido aconteça quando o resultado dos dados for menor ou igual ao valor da Habilidade testada. Dá pra ver que podemos ter onze opções de níveis de Habilidades, que vão desde 2 a 12 – o que pode ser interessante, se você quer um pouco mais de detalhes.
Há uma outra informação interessante aí: o valor mais provável de se obter – ou seja, aquele que tem maiores chances de aparecer no resultado dos dados – é 7, o que se revela como sendo o pico do primeiro gráfico. Você vai notar que isso aí ficou um pouco mais parecido com a famigerada curva do sino, que sempre falam por aí. O que faz ela interessante são as características acima, além de algumas que ainda vamos citar.
Exemplo
A distribuição de probabilidades pode te ajudar a tomar algumas decisões iniciais a respeito do seu sistema. Por exemplo, quais são as chances de sucesso de um personagem sem treinamento? Essa é, obviamente, uma questão que depende de uma série de fatores, mas você pode partir daqui.
Por exemplo, se você quer diferentes tipos de Habilidades (Fáceis, Normais e Difíceis), pode atribuir diferentes níveis iniciais para cada uma delas. Habilidades Fáceis podem ter nível inicial igual a 7 (mais ou menos 60% de chances de sucesso), Normais podem ter nível inicial igual a 6 (mais ou menos 40% de chances de sucesso), e Difíceis igual a 5 (por volta de 28% de chances).
Você pode, é claro, escolher valores diferentes que estejam mais de acordo com a sua visão, e a análise vai ter resultados diferentes para outros métodos de jogar os dados, mas a análise da distribuição de probabilidade vai te dar uma compreensão muito maior do que o seu sistema faz.
Exemplo
O sistema GURPS é bem semelhante ao que descrevemos aqui, mas usa 3d6 em seus testes. Habilidades normais nesse sistema tem nível pré-definido igual a 10, o que dá uma probabilidade de 50% de sucesso em um teste.
Mas há mais coisas interessantes aqui: dá pra ver que um personagem com Habilidade 7 é bem mais efetivo que um personagem com Habilidade 6 – o salto de 6 para 7 no segundo gráfico é bem grande. Não é a mesma diferença que acontece de 10 para 11. Isso significa que um personagem com Habilidade em nível 10 tem mais dificuldade para melhorar que um personagem de nível 6!
Exemplo
Um personagem com Habilidade 7 tem 21/36, enquanto o personagem com Habilidade 6 tem 15/36 chances – isso é 40% a mais de chances de sucesso! Já um personagem de Habilidade 11 tem 35/36 chances de sucesso, quando o personagem com Habilidade 10 tem 33/36 – isso é apenas um pouco mais de 6% de melhora. Isso é bastante realista, pois as coisas são assim na realidade: quanto mais você sabe sobre algo, mais difícil é aprender algo novo.
Para calcular esses valores, divida as chances de 7 pelas chances de 6: isso é (21/36) / (15/36) – use uma calculadora para facilitar sua vida. O resultado (multiplicado por 100%) é de 120%, o que indica 20% de melhora. Repita o procedimento para os personagens de 10 e 11 para constatar o resultado.
Mas o interessante dessa distribuição é que esse acréscimo decrescente aparece naturalmente, e você não precisa ajustar tabelas de níveis de experiência para simular a dificuldade de aprendizado para pessoas muito experientes. É bastante aconselhável, quando você estiver projetando seu sistema, tentar procurar por esse tipo de característica: deixe que a estrutura do sistema faça o trabalho pesado, ao invés de seus jogadores.
Ufa, esse foi pesado. Falaremos mais ainda em um próximo artigo.
Adendo: Como Calcular Essa Distribuição de Probabilidades?
Calcular probabilidades é uma coisa difícil. Existem diversas técnicas para isso, mas elas são complicadas. Sério, é difícil pra caramba. Se você realmente quer se aprofundar nisso, procure informações a respeito de Análise Combinatória e Experimentos de Bernoulli para começar.
No entanto, uma maneira garantida de obter distribuições de probabilidade é listar todas as possibilidades e contar. Isso é muito trabalhoso para muitos dados (é preferível usar um computador nesses casos, e vamos explorar isso em um artigo futuro), mas para o caso de dois dados de 6 faces, pode ser feito em uma tabela simples.
As colunas representam o resultado do primeiro dado; as linhas o resultado do segundo dado. No encontro, o resultado da soma. Dá pra ver que existem 4 formas diferentes de obter o resultado 5 em 36 possíveis – portanto, a probabilidade é 4/36.
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |