Análise das Probabilidades no Scop

Antes de decidir se você quer usar o Scop em seu cenário, talvez você queira dar uma olhada com um pouco mais de profundidade em como a jogada de dados se comporta. Ou, em outras palavras, quais são as chances de sucesso em uma Tarefa?

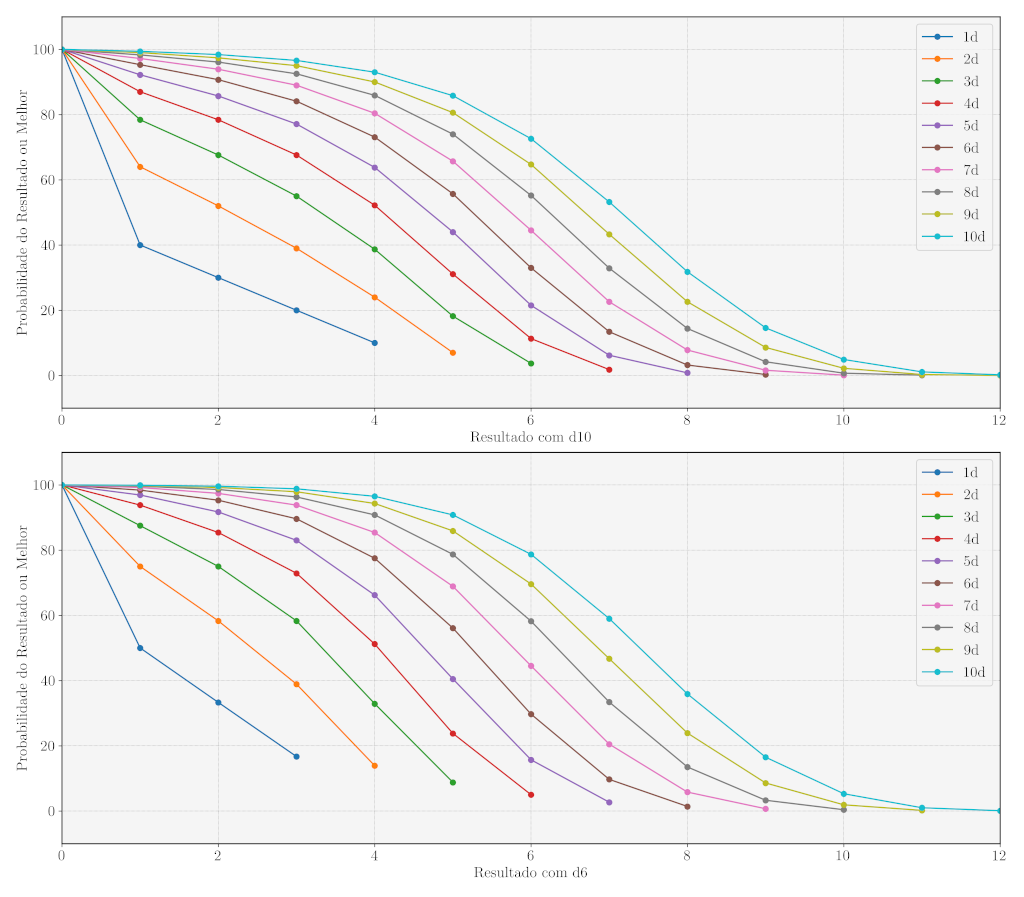
O gráfico abaixo mostra as probabilidades (dê uma outra olhada na jogada de dados se você não se lembra como ela funciona). Como no Scop, bônus e penalidades afetam, primordialmente, a quantidade de dados jogados, é fácil interpretar o gráfico abaixo. Cada linha colorida é o comportamento da jogada para uma certa quantidade de dados, e cada valor na horizontal mostra a probabilidade de obter aquele valor ou mais.

Por exemplo, a linha mais baixa, em preto, indica os resultados possíveis jogando apenas um dado. A probabilidade de obter 1 ou mais é exatamente 40%, de obter 2 ou mais é 30%, de obter 3 ou mais é 20%, e de obter 4 ou mais é 10%. Não é possível obter 5 ou mais usando um dado apenas. As outras curvas se comportam exatamente da mesma forma.

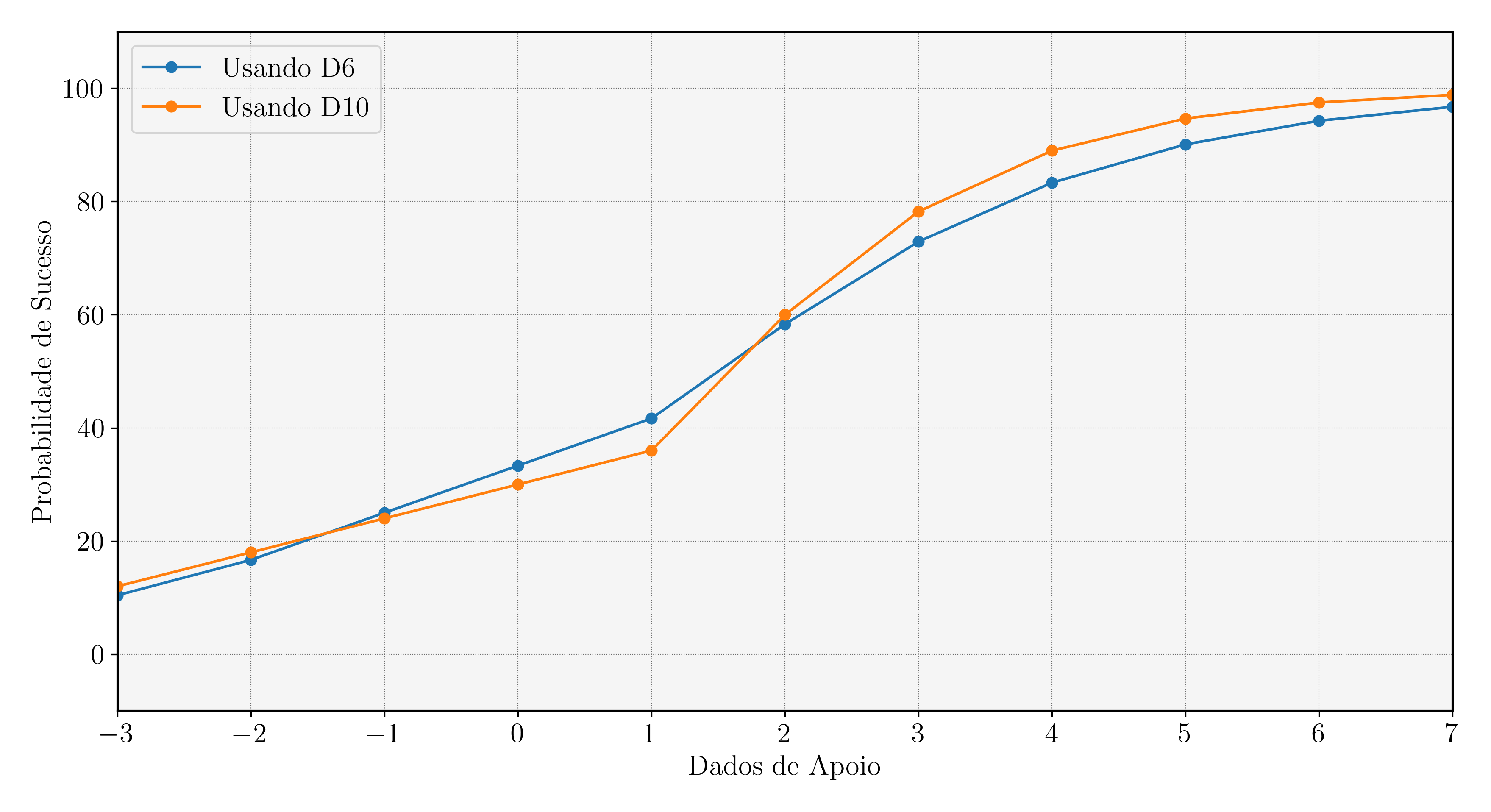
Dá pra ver que, jogando dois dados, a probabilidade de obter 3 ou mais é de cerca de 40%. Ou seja, uma pessoa mediana tentando uma tarefa simples tem mais ou menos 40% de chances de ser bem-sucedida. Se você seguir as curvas na vertical, vai ver que essas chances vão aumentando conforme você aumenta o número de dados. De fato, a probabilidade de obter 3 ou mais são exatamente as seguintes:

(Já que é possível jogar o Scop usando tanto dados de 10 lados quanto de 6 lados, estamos mostrando os resultados aqui para as duas situações. Veja como são parecidas!)

Então, um personagem realizando uma Tarefa com dificuldade normal, com dois Conceitos aplicáveis, e uma Habilidade em +2, jogando no total 6 dados, tem 84% de chances de ser bem-sucedido.

Uma vez que, no Scop, o valor exato do resultado pode ser usado para conceder bônus, penalidades, afetar outras jogadas e, de maneira geral, indicar a capacidade do seu personagem, é interessante analisarmos a média do resultado. A média é o que você esperaria obter como resultado caso os resultados da jogada fossem sempre iguais (não é exatamente isso, mas é uma interpretação útil):

Dá pra ver que a média cresce relativamente rápido para poucos dados, mas depois o crescimento é um pouco mais lento. Isso é em geral desejável em uma mecânica de dados, pois representa bem a curva de aprendizado: as coisas são aprendidas mais rapidamente quando o conhecimento é escasso; depois as coisas ficam mais difíceis.

Essas probabilidades foram calculadas utilizando o excelente site Anydice. Ao clicar no link, o programa vai abrir, mostrando resultados mais completos para você analisar como quiser (e testar algumas modificações, se tiver a inclinação para isso). Não se esqueça de fazer uma doação! Se você tiver algum problema com o programa, copie o texto abaixo, cole na janela de script, e clique em Calculate.

function: cut R:n at T:n {
  if R <= T { result: R }
  result: 0
}

function: decide R:s {
  if 1@R = 0 { result: 0 }
  result: 1@R + (R > 0) - 1
}

D: [ cut 1d10 at 4 ]
loop M over { 1..10 } {
   output [ decide MdD ] named "[M]d10"
}

E: [ cut 1d6 at 3 ]
loop M over { 1..10 } {
   output [ decide MdE ] named "[M]d6"
}